Daniel Bernoulli biography

Daniel Bernoulli (January 29, 1700 – March 17, 1782) mathematician, statistician, physicist, and physician. He was born in Groningen, Holland. His father, Johann Bernoulli, was a researcher who made important contributions to the early development of calculus. The family had to flee to the Netherlands due to the persecution of the Huguenots. After a brief period in Frankfurt, they settled in Basel, Switzerland. Bernoulli was always a very intelligent and curious young man. In high school, he achieved notable qualifications and mastered three languages, upon graduation he entered the university to study medicine and obtained his degree in 1721 thanks to his thesis on breathing where he assumed the mechanistic approach that prevailed at the time and was closer of his intellectual inclinations.

As soon as he graduated he tried to enter as a professor at the University of Basel but was rejected. Subsequently, Daniel was invited to work at the St. Petersburg Academy of Sciences, as a professor of mathematics. In this place, he met the great mathematician Leonhard Euler and then became his collaborator. He corresponded with the Prussian mathematician Christian Goldbach, most of the correspondence was about the lessons learned with his father, dazzled by the level of Bernoulli, decided to publish the letters written by Daniel.

From 1731 he began research on the problems of life and health from the statistics. Two years later he returned to Basel where he served as professor of anatomy, botany, philosophy, and physics. Simultaneously, he advanced important hydrodynamic studies, for Bernoulli this was one of the most important properties of fluid flow, pressure, density, and velocity.

From these studies arose The Bernoulli Principle or the Dynamic Theory of fluids. In his theory, he gave a masterly explanation about the pressure of the gas on the walls of a container. Because of the above, he obtained a remarkable amount of prizes and recognition between 1725 and 1749. He also obtained many more for his studies in astronomy, gravity, tides, magnetism, ocean currents and the behavior of a boat in the sea. It is notorious that he maintained a bad relationship with his father from 1734, the year in which both shared the annual prize of the Academy of Sciences of Paris.

Johann came to expel him from his home and also published a book called Hydraulica in which he tried to attribute the discoveries of his son in this matter. His popularity and intelligence earned him a place at the University of Basel, in the chair that his father had occupied. During this period as a professor, he published 86 papers and won 10 prizes from the Paris Academy of Sciences. Later he was a member of the Royal Society from May 3, 1750. He always thought a lot about students who could not access education due to lack of resources, for that reason he advanced the construction of a pension for the shelter of students without resources, This was maintained until the end of his days with his money. In addition, while he was rector of the University of Basel, in 1744 and 1756.

He was very committed to the development of the University. He made monetary donations on several occasions for laboratory equipment and acquisition of new titles in the Library. His prestige grew considerably both as a lecturer in Theoretical Physics and especially for his uncommon classes of Experimental Physics. Normally his conferences were attended by more than one hundred participants, from different corners of Europe.

He is considered one of the precursors of the kinetic theory of gases. He proposed a model of the structure of gases, in which he assumed that atoms in continuous motion collided with each other and with the walls of the container that contains them; that approach was the starting point of the kinetic theory of gases. Bernoulli also analyzed the problem of analyzing the errors in the observations. Bernoulli showed the insufficiency of the reasoning handled at that time and advised to use a method that can be considered an antecedent to the method of least squares reformulated later by Gauss.

At present, and based on the studies of his texts, it is noticed that he was able to find in the Mathematical Analysis the means to extract from the calculations all the details of the phenomena. Daniel Bernoulli suffered a cardiac arrest on March 17, 1782, in Basel, this episode did not allow him to stay alive. At his funeral he was dismissed by hundreds of colleagues and relatives at a solemn ceremony of the Academy of Sciences of Paris organized by the philosopher and geometer Marqués de Condorcet, who then served as Perpetual Secretary, he also read a funeral eulogy that collects the merits of his work and also his characteristics as a true man of science.

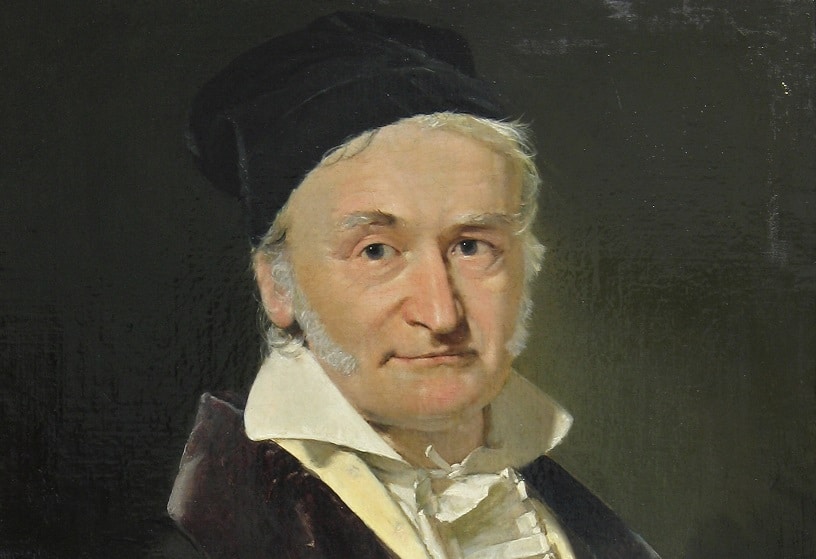
Carl Gauss biography

Johann Carl Friedrich Gauss (May 4, 1777 – February 23, 1855), mathematician, physicist, and German astronomer. He was born in Brunswick, Germany. His full name is Johann Friedrich Carl Gauss. Although in the world it is known as Carl Gauss. He was the son of a humble couple, made up of Geghard Dietrich Gauss and Dorothea Benze. His father was a gardener. For her part, her mother was raised in the homes of wealthy families.

From the age of three, he showed his genius, being very skilled in mathematical operations, which in his family had not been taught by the lack of illustration of his parents. The boy was sent to a precarious school, where he quickly learned to read and write. As he moved forward, he embraced broader aspirations, he asked his father to admit him to the school run by J.G Büttner, the Katherine Volkschule. This school governed by extreme discipline was a favorable space to exploit their ingenuity. In an arithmetic class, Carl Gauss had surprised his classmates and professor by answering a complex problem, which would later be known as the algorithm of the sum of the terms.

Gauss worked with Martin Bartels. Despite the age difference, Bartels took him almost 10 years, together they worked in mathematics. This little boy learned from Bartels, topics such as Newton’s binomial for non-integer exponents. This was key to his future. Then, enter the Gymnasium Catharineum, despite the refusal of his father. There he studied Latin and Greek.

When finishing his studies, he begins to be known in the illustrated circles of Brunswick. His name will reach the ears of Duke Karl Wilhelm Ferdinand. Thus, in 1791, he is sponsored by Zimmerman, professor of Collegium Carolinum and provincial advisor to the duke. The duke, impacted and fascinated by the intellectual ability of the young Carl Gauss, provided him with the funds to continue his training. Interested in his performance, he gave him the logarithm tables elaborated by Johann Carl Schulze.

Gauss remained most of the time doing mathematics readings like Principia Mathematica by Isaac Newton, Ars Conjectandi by Jakob Bernoulli and some of Euler’s memoirs. In the Collegium Carolinum Gauss will initiate some of his future mathematical investigations related to the distribution of prime numbers or the fundamentals of geometry. In 1795 he moved to the Georgia Augusta University of Göttingen, with a scholarship from the Duke. There he met Wolfgang Bolyai, this was one of the few characters who managed to interpret his metaphysical criteria about Mathematics.

Carl Gauss returned to his home in Brunswick, where he made a discovery that was key: the heptadecágono, a regular 17-sided polygon built with ruler and compass. His discovery was noted by him with great enthusiasm in his diary, a small notebook, which accompanied Gauss all his life. This would be the most important scientific journal in the history of mathematics, in it is a high percentage of mathematical discoveries of the nineteenth century.

Thanks to the Duke, this young man was able to build his work called the Disquisitiones Arithmeticae. But the benefits of the duke did not end here, helped Gauss to obtain a Ph.D. in philosophy at the University of Helmstedt. From the result of his thesis in 1849, he expanded his study on the field of variation of the coefficients to complex numbers.

Beginning in the 19th century, he reached the top of European mathematics and was recognized by the entire scientific community. Carl Gauss began his research on number theory during the Collegium Carolinum, in 1795. A year later he was able to decompose any whole number into three triangular ones and carried out the construction of the regular heptadecagon. This produced a new orientation to the Theory of Numbers, it became a branch of the most important mathematics.

In 1805, he married Johanna Osthoff with whom he will have three children: Joseph, Minna, and Louis. The following year, of the birth of his first son, he advanced with the French colonel Epailly the triangulation of Brunswick, which motivated his interest in geodesy. Later he was appointed professor at Gottingën and undertook the foundation of his astronomical observatory, which was interrupted by the Napoleonic occupation of the Germanic states.

After several years, he published the Theory of the movement of celestial bodies that revolve around the Sun following conic sections, published in 1809, a work consisting of two volumes, in these, deals: differential equations, conic sections, and elliptical orbits, explains its least-squares method for determining the orbit of a planet. He also presented his work Least Squares Method before the Royal Society of Gottingen. Theory of the combination of observations.

His wife died giving birth to her third child, and then her son will die only three months after birth. Carl Gauss married Minna Waldeck, Johanna’s friend, this union was born two sons Eugen and Wilhelm and a daughter Therèse. At this time he was already director of his observatory, he investigated infinite series, hypergeometric series, the approximation of integrals and statistical estimators.

For years, Gauss devoted his energies to tedious astronomical and geodetic calculations. His efforts were worthwhile because of this task will be born more than 70 writings on Geodesy: the application of the method of least squares to terrestrial measurements, the invention of the heliotrope, and the geometry of surfaces.

His curious spirit led him to visit railway works in Hannover, Gottingen to see technological progress. While there he suffered a serious accident in the horse carriage in which he was traveling. As of that moment, his health deteriorated considerably, dropsy was detected. Finally, on February 23, 1855, he died.

Bertrand Russell Biography

Bertrand Arthur William Russell, better known as Bertrand Russell, was born on May 18, 1872, in Trelleck (Wales) and died on February 2nd, 1970 at the age of 97 years.

Being six years old, Russell would become orphaned after the death of his sister and his mother, and later his father, in 1878. According to his own autobiography, his desire to learn more about mathematics was what got him away from suicide.

“At the age of 11, I started as a tutor of Euclid, my brother who was seven years older. It was one of the great events of my life, like the first love. I had not been able to imagine that there was anything so delicious in the world.”  Bertrand Russell

He began his education at Trinity College, Cambridge. Once he graduated, in 1888, he was sent to the United States to complement his studies and so that he could study the political life and institutions of the country.

In 1894, Russell would marry Alys Smith. However, the marriage did not last long.

He made his name popular with the Principles of Mathematics in 1902. Between 1910 and 1913, he wrote Principia Mathematica (Mathematical Principles), a work that has 3 volumes. His next great work was The Problems of Philosophy (1912), in which he turned to mathematics, sociology, psychology, and physics to refute the doctrines of idealism. In 1919, Bertrand Russell wrote Introduction to Mathematical Philosophy, and a year later he published The Practice and Theory of Bolshevism.

Bertrand Russell lived in Russia during 1920. Between 1921 and 1922 he worked as a professor at Peking University (China). During his stay in Beijing, he suffered from pneumonia, which led to it being rumored in several European newspapers that he had died. Also during this period, specifically in 1921, he married his second wife, Dora Black.

He returned to his country and published a series of texts that contributed to his national recognition: The Analysis of mind (1921) and The Analysis of Matter (1927). From 1928 to 1932, he directed the Beacon Hill School, a very progressive private school where innovative teaching methods for children were applied. In the United States, he wrote A History of Western Philosophy (1945).

For texts such as What I Believe (1925) and his defense of sexual freedom, manifested in Marriage and Morals (1929), The Conquest of Happiness (1930) and Education and the Social Order (1932), he was banned from teaching in New York, for what they considered attacks religion.

In 1950, Bertrand was awarded the Nobel Prize for Literature “In recognition of his varied and significant writings in which he has fought for humanitarian ideals and freedom of thought.”

In 1953, he published the novel Satan in the suburbs and other stories.

Bertrand Russell died on February 2, 1970, at his home, Plas Penrhyn, in Penrhyndeudraeth, Merionethshire, Wales. His body was incinerated in Colwyn Bay on February 5, 1970. According to his will, there was no religious ceremony; his ashes were scattered in the mountains of Wales.

Bertrand Russell could be just a brilliant mathematician who won a Nobel. But he also was a philosopher who, for his writings, won the prize in the category of Literature. He was an activist who defended the rights of women and who lost jobs for supporting sexual freedom at the beginning of the 20th century. He was a pacifist that rejected the First World War and was sent to jail. The one that opposed Hitler, Stalinism, the US invasion of Vietnam, nuclear bombs and racial segregation. The one who made peace, his struggle. Besides, Russell was the one that three months before his death, with 97 years, appealed to the Secretary-General of the United Nations to support a commission against the war crimes committed by the Americans in the Asian country.

Bertrand Russell was an intellectual in the broadest and deepest sense of the word.

“Three passions, simple but overwhelmingly intense, have ruled my life: the longing for love, the search for knowledge and an unbearable pity for the suffering of humanity” Bertrand Russell.

Russell considered the intellectual’s mission to spread a culture that accustomed men to the revision of their own ideas and mutual tolerance. I knew that science, as such, is not enough for the happiness of human beings, who, in the pursuit of this goal, must resort to art, to love and to reciprocal respect.

His theory of knowledge is real and wants to connect with the intuitions of ordinary common sense. On one hand, he is the heir of the old tradition of British empiricism, a philosophical current always linked to the spirit of liberalism and the Enlightenment, which aims to reduce all cognitive content to the data of sensory experience. On the other hand, he is the most ambitious contemporary logician, obsessed with the idea of ​​a perfect symbolic language that eliminates all expressive ambiguity. The result of all these concerns is the so-called Russell’s logical atomism.

Evangelista Torricelli Biography

Evangelista Torricelli (1608-1647) was an Italian physicist and mathematician who made great contributions in the fields of pure mathematics, integral calculus and the movement of projectiles and fluids. Evangelista Torricelli thought that mathematics was the language that allowed humans to understand nature.

Torricelli was the first man to recognize that air has weight and that atmospheric pressure is variable. From this idea, he created an artifact that was known as Torricelli’s tube and that gave rise to the invention of the barometer. On the other hand, in the field of mathematics, Evangelista developed hat is called Torricelli’s theorem which helps to calculate the flow of a liquid through an open hole at a certain depth.

Evangelista Torricelli was born on October 15, 1608, in Faenza, province of Ravenna, Italy, and grew up in a humble family. His parents were Gaspare Torricelli, a textile worker, and Caterina Angetti. When their parents realized his potential, they decided to send him to study humanities with his father’s brother, Jacobo, who was a Camaldulense friar.

In 1624, he entered a Jesuit college where he was taught in mathematics and philosophy for two years. After his father died, between 1626 and 1627 he traveled to Rome with his whole family (his mother and two brothers) to study with the Benedictine friar, Benedetto Castelli.

Torricelli would be assigned the position of private secretary of Castelli. He used the money obtained with work to pay for his studies so he could stay in the position and studying at the University College of Sapienza until 1632. Later, Castelli appointed Torricelli to replace him as the teacher in mathematics, mechanics, hydraulics, and astronomy in the University College of Sapienza.

On September 11, 1632, Torricelli received a letter from Galileo addressed to Castelli. In his response, Torricelli besides explaining the reason for the absence of his teacher, he took the opportunity to express his admiration for the text Dialogue Concerning the Two Chief World Systems, Ptolemaic and Copernican that was written by Galileo six months earlier, and presented his support for the Copernicus theory that the earth revolves around the sun.

After Galileo was ordered to appear in Rome for his astronomy approaches, Torricelli decided to move his attention to less dangerous terrain, so he concentrated on mathematics.

In De Motu Gravium et Levium, Torricelli consigned some developments to the mechanical principles set forth by Galileo in his book Two New Sciences (1638). Shortly afterward, on April 10th, 1641, Castelli handed Galileo a copy of this work, and later, Torricelli became Secretary of Galileo. Unfortunately, after three months of coexistence with Galileo in Florence, Galileo passed away.

In spite of the death of Galileo, he remained in Florence as a philosopher and mathematician of the Grand Duke Ferdinand II and professor of mathematics at the Academy. Shortly after, he managed to answer the question that had haunted Galileo: the question of the veracity of Aristotle’s theory, which said that Nature abhors a vacuum.

Torricelli achieved the answer by means of an experiment that consisted of filling a tube with mercury (liquid that is 13.5 times denser than water) covering one end of the container and inserting it into another container with more mercury. In this way, it was observed that a part of the mercury that filled the tube is transferred to the second container creating a space for the vacuum. In addition, his demonstration of the existence of emptiness included the clarity that it is not possible to find it in nature but it is necessary to generate it artificially.

In 1643, he demonstrated the existence of atmospheric pressure and developed the basis for the barometer.

The barometer was not Torricelli’s only important discovery. For example, thanks to him we know that geometric curves are not limited to their theoretical form but are representations of real physical movements. From this idea, it was proposed to study the parabolic trajectories followed by the projectiles when being fired and reached two conclusions: the first was that “the envelope of all these parables is another parable” and the second was that “the locus of the vertices of all the parabolas is also another parabola.” Apart from this, he showed that “the rotation of curves of infinite length can produce solids of finite volume.” (Suma, 2009).

Undoubtedly Torricelli was one of the most productive and promising mathematicians of the seventeenth century. It is believed that if he had not died so young (he was only 39 years old at the time of his death) he would have formulated his methods mathematically and would have approached the concept of the limit. It is even believed that he could have invented the infinitesimal calculus. Unfortunately, he lost the battle against pleurisy in 1647, and died in Florence, Italy.